[এই অধ্যায়ের প্রয়োজনীয় পূর্বজ্ঞান বইয়ের শেষে পরিশিষ্ট অংশে সংযুক্ত আছে। প্রথমে পরিশিষ্ট অংশ পাঠ/আলোচনা করতে হবে।]
আমাদের চারদিকে বিভিন্ন আকৃতি ও আকারের বস্তু দেখতে পাই। এদের কিছু হুবহু সমান, আবার কিছু দেখতে একই রকম, কিন্তু সমান নয়। তোমাদের শ্রেণির শিক্ষার্থীদের প্রত্যেকের গণিত পাঠ্যপুস্তুকটি আকৃতি, আকার ও ওজনে একই, সেগুলো সবদিক দিয়ে সমান বা সর্বসম। আবার একটি গাছের পাতাগুলোর আকৃতি একই হলেও আকারে ভিন্ন, পাতাগুলো দেখতে এক রকম বা সদৃশ। ফটোগ্রাফির দোকানে যখন আমরা মূলকপির অতিরিক্ত কপি চাই তা মূলকপির হুবহু সমান, বড়ো বা ছোটো করে চাইতে পারি। কপিটি যদি মূলকপির সমান হয় সেক্ষেত্রে কপি দুটি সর্বসম। কপিটি যদি মূলকপির চেয়ে বড়ো বা ছোটো হয় সেক্ষেত্রে কপি দুটি সদৃশ। এই অধ্যায়ে আমরা অত্যন্ত গুরুত্বপূর্ণ এই দুই জ্যামিতিক ধারণা নিয়ে আলোচনা করব। আমরা আপাতত সমতলীয় ক্ষেত্রের সর্বসমতা ও সদৃশতা বিবেচনা করব।
অধ্যায় শেষে শিক্ষার্থীরা -
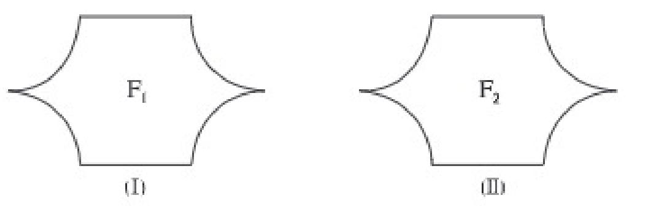
নিচের সমতলীয় চিত্র দুটি দেখতে একই আকৃতি ও আকারের। চিত্র দুটি সর্বসম কিনা নিশ্চিত হওয়ার জন্য উপরিপাতন পদ্ধতি গ্রহণ করা যায়। এ পদ্ধতিতে প্রথম চিত্রের একটি অনুরূপ কপি করে দ্বিতীয়টির উপর রাখি। যদি চিত্রগুলো পরস্পরকে সম্পূর্ণরূপে আবৃত করে, তবে এরা সর্বসম। চিত্র F1, চিত্র F2 এর সর্বসম হলে আমরা F1 ≅ F2 দ্বারা প্রকাশ করি।
দুটি রেখাংশ কখন সর্বসম হবে? চিত্রে দুই জোড়া রেখাংশ আঁকা হয়েছে। উপরিপাতন পদ্ধতিতে AB এর অনুরূপ কপি CD এর উপর রেখে দেখি যে, AB রেখাংশ CD রেখাংশকে ঢেকে দিয়েছে এবং A ও B বিন্দু যথাক্রমে C'ওD বিন্দুর উপর পতিত হয়েছে। সুতরাং রেখাংশ দুটি সর্বসম। একই কাজ দ্বিতীয় জোড়া সরলরেখার জন্য করে দেখি যে, রেখাংশ দুটি সর্বসম নয়। লক্ষ করি, কেবল প্রথম জোড়া রেখাংশের দৈর্ঘ্য সমান।

| দুটি রেখাংশের দৈর্ঘ্য সমান হলে রেখাংশ দুটি সর্বসম। আবার বিপরীতভাবে, দুটি রেখাংশ সর্বসম হলে এদের দৈর্ঘ্য সমান। |
দুইটি কোণ কখন সর্বসম হবে? চিত্রে 40° দুইটি কোণ আঁকা হয়েছে। উপরিপাতন পদ্ধতি গ্রহণ করে প্রথম চিত্রের একটি অনুরূপ কপি করে দ্বিতীয়টির উপর রাখি। B বিন্দু Q বিন্দুর উপর এবং BA রশ্মি QP রশ্মির ওপর পতিত হয়েছে। লক্ষ করি, কোণ দুটির পরিমাপ সমান বলে BC রশ্মি QR রশ্মির উপর পতিত হয়েছে। অর্থাৎ ∠ABC ≅ ∠PQR
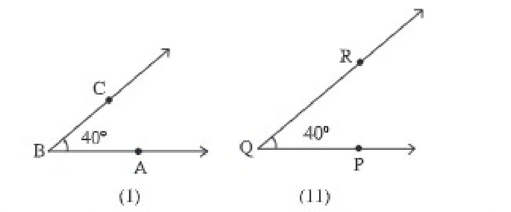
| দুটি কোণের পরিমাপ সমান হলে কোণ দুটি সর্বসম। আবার বিপরীতভাবে, দুটি কোণ সর্বসম হলে এদের পরিমাপও সমান। |
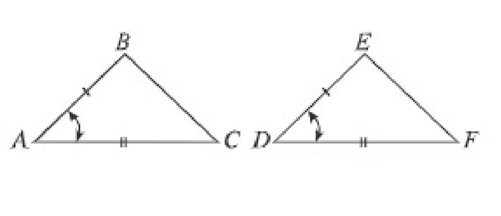
একটি ত্রিভুজকে অপর একটি ত্রিভুজের উপর স্থাপন করলে যদি ত্রিভুজ দুটি সর্বতোভাবে মিলে যায়, তবে ত্রিভুজ দুটি সর্বসম হয়। সর্বসম ত্রিভুজের অনুরূপ বাহু ও অনুরূপ কোণগুলো সমান। নিচের ABC ও DEF সর্বসম।

ABC ও DEF সর্বসম হলে এবং A, B, C শীর্ষ যথাক্রমে D, E, F শীর্ষের উপর পতিত হলে AB = DE , AC = DF BC = EF
∠ A = ∠ D ∠ B = ∠ E ∠ C = ∠ F হবে।
ABC ও DEF সর্বসম বোঝাতে ABC ≅ DEF লেখা হয়।
ত্রিভুজের সর্বসমতা প্রমাণের জন্য কী তথ্য প্রয়োজন? এ জন্য দলগতভাবে পরের পৃষ্ঠার কাজটি কর:
| কাজ ১। ∆ABC একটি ত্রিভুজ আঁক যেন AB =5 সে.মি., BC=6 সে.মি.এবং ∠B=60° হয়। (ক) ত্রিভুজের তৃতীয় বাহুর দৈর্ঘ্য এবং অন্য কোণ দুটি পরিমাপ কর। (খ) তোমাদের পরিমাপগুলো তুলনা কর। কী দেখতে পাচ্ছ? |
উপপাদ্য ১ (বাহু-কোণ-বাহু উপপাদ্য)
যদি দুটি ত্রিভুজের একটির দুই বাহু যথাক্রমে অপরটির দুই বাহুর সমান হয় এবং বাহু দুটির অন্তর্ভুক্ত কোণ দুটি পরস্পর সমান হয়, তবে ত্রিভুজ দুটি সর্বসম হয়।
বিশেষ নির্বচন: মনে করি,
বিশেষ নির্বচন: মনে করি,
ABC ও DEF এ AB = DE AC = DF এবং অন্তর্ভুক্ত ∠ BAC = অন্তর্ভুক্ত ∠ EDF প্রমাণ করতে হবে যে, ABC ≅ DEF
প্রমাণ
ধাপ | যথার্থতা |
| (১) ∆ABC কে Delta*DEF এর উপর এমনভাবে স্থাপন করি যেন A বিন্দু D বিন্দুর উপর ও AB বাহু DE বাহু বরাবর এবং DE বাহুর যে পাশে F আছে C বিন্দু ঐপাশে পড়ে। এখন AB = DE বলে B বিন্দু অবশ্যই E বিন্দুর উপর পড়বে। | [ বাহুর সর্বসমতা] |
| (২) যেহেতু angle BAC = angle EDF এবং AB বাহু DE বাহুর উপর পড়ে, সুতরাং AC বাহু DF বাহু বরাবর পড়বে। | [কোণের সর্বসমতা] |
| (৩) AC = DF বলে C বিন্দু অবশ্যই F বিন্দুর উপর পড়বে। | [ বাহুর সর্বসমতা] |
(৪) এখন B বিন্দু E বিন্দুর উপর এবং C বিন্দু F বিন্দুর উপর পড়ে বলে BC বাহু অবশ্যই EF বাহুর সাথে পুরোপুরি মিলে যাবে। অতএব, ABC, DEF এর উপর সমাপতিত হবে। ABC ≅ DEF (প্রমাণিত) | [দুটি বিন্দুর মধ্য দিয়ে একটি মাত্র সরলরেখা অঙ্কন করা যায়।] |
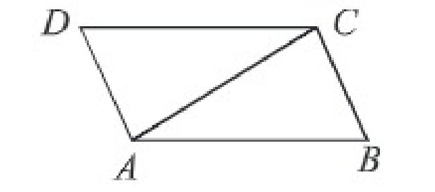
উদাহরণ ১। চিত্রে, AO = OB, CO = OD
প্রমাণ কর যে, ∆AOD ≅ ∆BOC
প্রমাণ: ∆AOD এবং ∆BOC এ
AO = OB, CO = OD দেওয়া আছে
এবং তাদের অন্তর্ভুক্ত ∠AOD = অন্তর্ভুক্ত ∠BOC
[বিপ্রতীপ কোণ পরস্পর সমান]।
∴ ∆AOD = ∆BOC [বাহু-কোণ-বাহু উপপাদ্য) (প্রমাণিত)

যদি কোনো ত্রিভুজের দুটি বাহু পরস্পর সমান হয়, তবে এদের বিপরীত কোণ দুটিও পরস্পর সমান হবে।
বিশেষ নির্বচন: মনে করি, ABC ত্রিভুজে AB = AC।
প্রমাণ করতে হবে যে, ∠ABC = ∠ACB
অঙ্কন: BAC এর সমদ্বিখণ্ডক AD আঁকি যেন তা BC কে D বিন্দুতে ছেদ করে।
প্রমাণ: ∆ABD এবং ∆ACD এ
(১) AB = AC (প্রদত্ত)
(২) AD সাধারণ বাহু এবং
(৩) অন্তর্ভুক্ত ∠BAD = অন্তর্ভুক্ত ∠CAD (অঙ্কনানুসারে)
সুতরাং ∆ABD ≅ ∠ACD (বাহু-কোণ-বাহু উপপাদ্য
∴ . ∠ABD = ∠ACD অর্থাৎ, ∠ABC = ∠ACB (প্রমাণিত)

১। চিত্রে, CD, AB এর লম্ব সমদ্বিখণ্ডক, প্রমাণ কর যে ADC ≅ ∠BDC

২। চিত্রে, CD = CB এবং ∠DCA = ∠BCA প্রমাণ কর যে, AB = AD

৩। চিত্রে, ∠BAC = ∠ACD এবং AB = DC প্রমাণ কর যে, AD = BC, ∠CAD = ∠ACB এবং ∠ADC = ∠ABC
৪। প্রমাণ কর যে, সমদ্বিবাহু ত্রিভুজের সমান বাহু বাদে অপর বাহু উভয়দিকে বর্ধিত করলে উৎপন্ন বহিঃস্থ কোণ দুটি পরস্পর সমান।
৫। চিত্রে, AD = AE, BD = CE এবং ∠AEC = ∠ADB প্রমাণ কর যে, AB = AC
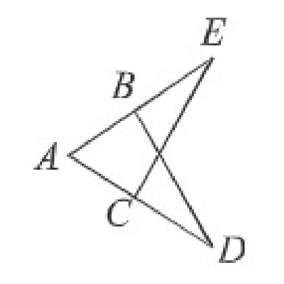
৬। চিত্রে, ∆ABC এবং ∆DBC দুটি সমদ্বিবাহু ত্রিভুজ। প্রমাণ কর যে, ∆ABD = AACD
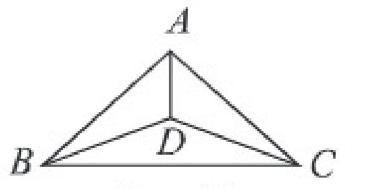
৭। প্রমাণ কর যে, সমদ্বিবাহু ত্রিভুজের ভূমির প্রান্তবিন্দু থেকে বিপরীত বাহুদ্বয়ের উপর অঙ্কিত মধ্যমাদ্বয় সমান।
৮। প্রমাণ কর যে, সমবাহু ত্রিভুজের কোণগুলো পরস্পর সমান।
উপপাদ্য ৩ (বাহু-বাহু-বাহু উপপাদ্য)
যদি একটি ত্রিভুজের তিন বাহু যথাক্রমে অপর একটি ত্রিভুজের তিন বাহুর সমান হয়, তবে ত্রিভুজ দুটি সর্বসম হবে।
বিশেষ নির্বচন: মনে করি, ∆ABC এবং ∆DEF এ AB = DE, AC = DF এবং BC = EF, প্রমাণ করতে হবে যে, ∆ABC ≅ ∆DEF
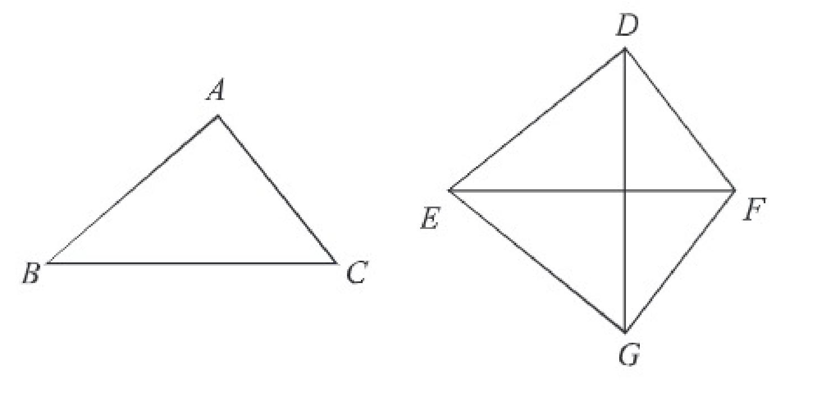
প্রমাণ: মনে করি, BC এবং EF বাহু যথাক্রমে ∆ABC এবং ∆DEF এর বৃহত্তম বাহুদ্বয়।
এখন ∆ABC কে ∆DEF এর উপর এমনভাবে স্থাপন করি, যেন B বিন্দু E বিন্দুর উপর ও BC বাহু EF বাহু বরাবর এবং EF রেখার যে পাশে D বিন্দু আছে, A বিন্দু এর বিপরীত পাশে পড়ে। মনে করি, G বিন্দু A বিন্দুর নতুন অবস্থান।
যেহেতু BC = EF, Cবিন্দু F বিন্দুর উপর পড়বে। সুতরাং ∆GEF হবে ∆ABC এর নতুন অবস্থান। অর্থাৎ, EG = BA, FG=CA ও ∠EGF = ∠BAC D, G যোগ করি।
| ধাপ | যথার্থতা |
| (১) ∆EGD এ EG = ED [কারণ EG = BA = ED] অতএব, ∠EDG = ∠EGD | [ত্রিভুজের সমান বাহুদ্বয়ের বিপরীত কোণ পরস্পর সমান] |
| (২) ∆FGD এ FG = FD অতএব, ∠FDG = ∠FGD | [ত্রিভুজের সমান বাহুদ্বয়ের বিপরীত কোণদ্বয় পরস্পর সমান। |
(৩) সুতরাং, ∠EDG + ∠FDG = ∠EGD + ∠FGD বা, ∠EDF = ∠EGF অর্থাৎ, ∠BAC = ∠EDF ∴∆ABC = ∆DEF (প্রমাণিত)। | [বাহু-কোণ-বাহু উপপাদ্য] |
উপপাদ্য ৪ (কোণ-বাহু-কোণ উপপাদ্য)
যদি একটি ত্রিভুজের দুটি কোণ ও কোণ সংলগ্ন বাহু যথাক্রমে অপর একটি ত্রিভুজের দুটি কোণ ও কোণ সংলগ্ন বাহুর সমান হয়, তবে ত্রিভুজ দুটি সর্বসম হবে।
বিশেষ নির্বচন: মনে করি, ∆ABC = ∆DEF -এ ∠B∠E, ∠C = ∠F এবং কোণ সংলগ্ন BC বাহু = অনুরূপ EF বাহু।

প্রমাণ করতে হবে যে, ∆ABC = ∆DEF
প্রমাণ
| ধাপ | যথার্থতা |
(১) ∆ABC কে ADEF এর উপর এমনভাবে স্থাপন করি যেন, B বিন্দু E বিন্দুর উপর ও BC বাহু EF বাহু বরাবর এবং EF রেখার যে পাশে D আছে বিন্দু A বিন্দু যেন ঐপাশে পড়ে। যেহেতু BC = EF, অতএব C বিন্দু F বিন্দুর উপর অবশ্যই পড়বে। | [ বাহুর সর্বসমতা] |
| (২) আবার, ∠B = ∠E বলে, BA বাহু ED বাহু বরাবর পড়বে এবং ∠C=∠F বলে, CA বাহু FD বাহু বরাবর পড়বে। | |
(৩)∴ BA এবং CA বাহুর সাধারণ বিন্দু A, ED ও FD বাহুর সাধারণ বিন্দু D এর উপর পড়বে। অর্থাৎ, ∆ABC, ∆DEF এর উপর সমাপতিত হবে। ∴∆ABC ≅ ∆DEF (প্রমাণিত)। | [ কোণের সর্বসমতা] |
অনুসিদ্ধান্ত: একটি ত্রিভুজের একটি বাহু ও দুটি কোণ যথাক্রমে অপর একটি ত্রিভুজের একটি বাহু ও দুটি কোণের সমান হলে ত্রিভুজ দুটি সর্বসম।
কাজ 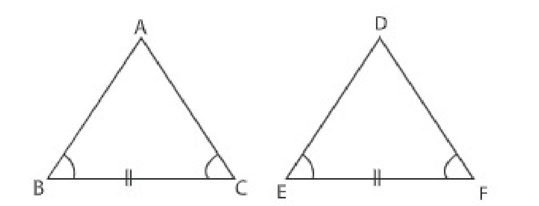 ∆ ABC ও ∆DEF এ BC=EF এবং ∠B=∠E ও ∠C=∠F হলে দেখাও যে, △ ABC ≅ ∆DEF ইঙ্গিত: ∠A+B+C= ∠D+∠E+∠F = ২ সমকোণ হবে। ∴ ∠B=∠E, ∠C=∠F, হলে ∠A=∠D হবে। অতঃপর উপপাদ্য 8 প্রয়োগ কর। |
উদাহরণ ১। প্রমাণ কর যে, কোনো ত্রিভুজের শিরঃকোণের সমদ্বিখণ্ডক যদি ভূমির উপর লম্ব হয়, তবে ত্রিভুজটি সমদ্বিবাহু।
বিশেষ নির্বচন: চিত্রে, ∆ABC এর শিরঃকোণ A-এর সমদ্বিখণ্ডক AD যা ভূমি BC এর D বিন্দুতে লম্ব। প্রমাণ করতে হবে যে, AB = AC
প্রমাণ: ∆ABD এবং ∆ACD এ ∠BAD = ∠CAD [∵AD, ∠BAC এর সমদ্বিখণ্ডক]
∠ADB = ∠ADC [: AD, BC এর উপর লম্ব]
এবং AD সাধারণ বাহু।
সুতরাং ∆ABD ≅ ∆ACD [কোণ বাহু কোণ উপপাদ্য। এতএব, AB = AC [প্রমাণিত]

উপপাদ্য ৫ (সমকোণী অতিভুজ-বাহু উপপাদ্য)
দুটি সমকোণী ত্রিভুজের অতিভুজদ্বয় সমান হলে এবং একটির এক বাহু অপরটির অপর এক বাহুর সমান হলে, ত্রিভুজদ্বয় সর্বসম হবে।

বিশেষ নির্বচন: মনে করি, ABCও DEF সমকোণী ত্রিভুজদ্বয়ে অতিভুজ AC =অতিভুজ DF এবং AB = DE প্রমাণ করতে হবে যে, ∆ABC ≅ ∆DEF
| ধাপ | যথার্থতা |
| (১) ∆ABC কে △DEF এর উপর এমনভাবে স্থাপন করি যেন, B বিন্দু E বিন্দুর উপর, BA বাহু ED বাহু বরাবর এবং C বিন্দু DE এর যে পাশে F বিন্দু আছে এর বিপরীত পাশে পড়ে। ধরি, C বিন্দুর নতুন অবস্থান G। | [ত্রিভুজের দুই বাহু সমান হলে তাদের বিপরীত কোণ দুটি পরস্পর সমান] |
| (২) যেহেতু AB=DE, A বিন্দু D বিন্দুর উপর পড়বে। ফলে △ DEG হবে ∆ABC এর নতুন অবস্থান অর্থাৎ DG AC, ∠G=∠C ∠DEG= ∠B = 1 সমকোণ। | |
(৩) যেহেতু ∠DEF+∠DEG = 1 সমকোণ + 1 সমকোণ = 2 সমকোণ = 1 সরলকোণ, GEF একটি সরলরেখা। সুতরাং △ DGF একটি সমদ্বিবাহু ত্রিভুজ। যার DG=DF ∴ ∠FZG=∠C | [কোণ-বাহু-কোণ উপপাদ্য |
| (৪) এখন △ ABC ও △DEF এর ∠B = ∠E [প্রত্যেকে ১ সমকোণ। ∠C = ∠F এবং AB = অনুরূপ DE সুতরাং △ ABC ≅ △DEF (প্রমাণিত) |
১। ∆ABC এ AB = AC এবং O, ABC এর অভ্যন্তরে এমন একটি বিন্দু যেন OB = OC হয় প্রমাণ কর যে, ∠AOB = ∠AOC
২। ∆ABC এর AB ও AC বাহুতে যথাক্রমে DওE এমন দুটি বিন্দু যেন BD = CE এবং BE = CD প্রমাণ কর যে, ∠ABC = ∠ACB
৩। চিত্রে, AB = AC, BD = DC এবং BE = CF | প্রমাণ কর যে, ∠EDB = ∠FDC

৪। চিত্রে, AB = AC এবং ∠ BAD = ∠ CAE । প্রমাণ কর যে, AD = AE
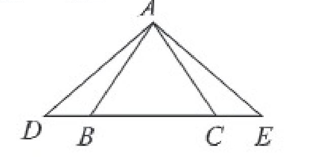
৫। ABCD চতুর্ভুজে AC, ∠ BAD এবং ∠ BCD এর সমদ্বিখণ্ডক। প্রমাণ কর যে, ∠ B = ∠ D
৬। চিত্রে, AB এবং CD পরস্পর সমান ও সমান্তরাল এবং AC ও BD কর্ণ দুটি বিন্দুতে ছেদ করেছে। প্রমাণ কর যে, AD = BC
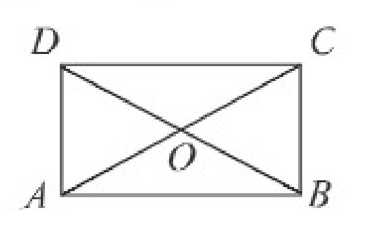
৭। প্রমাণ কর যে, সমদ্বিবাহু ত্রিভুজের ভূমির প্রান্তবিন্দুদ্বয় থেকে বিপরীত বাহুর উপর অঙ্কিত লম্বদ্বয় পরস্পর সমান।
৮। প্রমাণ কর যে, কোনো ত্রিভুজের ভূমির প্রান্ত বিন্দুদ্বয় থেকে বিপরীত বাহুর উপর অঙ্কিত লম্বদ্বয় যদি সমান হয়, তবে ত্রিভুজটি সমদ্বিবাহু।
৯। ABCD চতুর্ভুজের AB = AD এবং ∠B = ∠D = এক সমকোণ। প্রমাণ কর যে, ∆ABC ≅ AADC
নিচের চিত্রগুলো একই চিত্রের ছোটো-বড়ো আকার। এদের বিভিন্ন অংশের আকৃতি একই, কিন্তু অনুরূপ দুই বিন্দুর দূরত্ব সমান নয়। চিত্রগুলোকে সদৃশ চিত্র বলা হয়।

কাজ
১। (ক) চিত্রের ত্রিভুজ দুটি কি সদৃশ বলে মনে হয়?  (খ) ত্রিভুজ দুটির কোণগুলো মেপে সারণিটি পূরণ কর। কোণগুলোর মধ্যে কোনো সম্পর্ক আছে কি? (গ) ত্রিভুজ দুটির বাহুগুলো মেপে সারণিটি পূরণ কর। বাহুগুলোর মধ্যে কোনো সম্পর্ক আছে কি? |
পূরণকৃত ছকটি হতে দেখা যায়,
∠A = ∠L
∠B = ∠M
∠C=∠N
∠L,∠M ও ∠N যথাক্রমে ∠A, B, ও ∠C এর অনুরূপ কোণ।
আরো লক্ষ করা যায়
LM, MN ও NL বাহুগুলো যথাক্রমে AB, BC ও CA বাহুর অনুরূপ বাহু।
দুটি ত্রিভুজ বা বহুভুজ সদৃশ হলে
সদৃশ চিত্রের বাহুগুলোর অনুপাত দ্বারা মূল চিত্রের তুলনায় অন্য চিত্রের বর্ধন অথবা সঙ্কোচন বোঝায়।
সদৃশ চিত্র একই আকৃতির কিন্তু আকারে সমান নাও হতে পারে। সদৃশ চিত্রের আকার সমান হলে তা সর্বসম চিত্রে পরিণত হয়। সুতরাং সর্বসমতা সদৃশতার বিশেষ রূপ।
দুটি সদৃশ ত্রিভুজের অনুরূপ কোণগুলো সমান এবং অনুরূপ বাহুগুলো সমানুপাতিক। দুটি ত্রিভুজ সদৃশ হওয়ার জন্য ন্যূনতম শর্ত বের করি।
কাজ
|
আগের পৃষ্ঠার আলোচনা থেকে আমরা ত্রিভুজের সদৃশতার কতিপয় শর্ত নির্ধারণ করতে পারি। শর্তগুলো নিম্নরূপ:
শর্ত ১। (বাহু-বাহু-বাহু)
যদি একটি ত্রিভুজের তিন বাহু অপর একটি ত্রিভুজের তিন বাহুর সমানুপাতিক হয়, তবে ত্রিভুজ দুটি সদৃশ।

শর্ত ২। (বাহু-কোণ-বাহু)
যদি দুটি ত্রিভুজের একটির দুই বাহু যথাক্রমে অপরটির দুই বাহুর সমানুপাতিক হয় এবং বাহু দুটির অন্তর্ভুক্ত কোণ দুটি পরস্পর সমান হয়, তবে ত্রিভুজ দুটি সদৃশ।
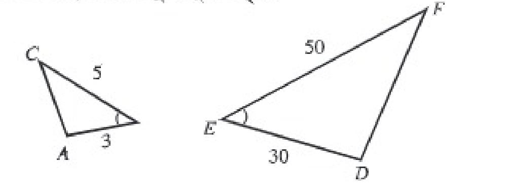
শর্ত ৩। (কোণ-কোণ)
যদি দুটি ত্রিভুজের একটির দুটি কোণ যথাক্রমে অপরটির দুটি কোণের সমান হয়, তবে ত্রিভুজ দুটি সদৃশ।

শর্ত ৪। (অতিভুজ-বাহু)
যদি দুটি সমকোণী ত্রিভুজের একটির অতিভুজ ও একটি বাহু যথাক্রমে অপরটির অতিভুজ ও অনুরূপ বাহুর সমানুপাতিক হয়, তবে ত্রিভুজ দুটি সদৃশ।

দুটি সদৃশ চতুর্ভুজের অনুরূপ কোণগুলো সমান এবং অনুরূপ বাহুগুলো সমানুপাতিক। দুটি চতুর্ভুজ সদৃশ হওয়ার শর্ত নির্ণয় করি।
| কাজ ১। তিন-চার জনের দল গঠন করে নিচের কাজগুলো কর: (ক) KLMN চতুর্ভুজটি আঁক, যার ∠ K = 45° KL = 3 সে.মি., LM = 2 সে.মি., MN = 3 সে.মি., NK = 2.5 সে.মি.। [ইঙ্গিত: প্রথমে ∠K কোণটি আঁক এবং কোণের বাহু দুটি থেকে KL ও KN সমান দূরত্বে দুটি বিন্দু চিহ্নিত কর। অতঃপর অপর দুই বাহু আঁক।। (খ) WXYZ চতুর্ভুজটি আঁক, যার WX = 6 সে.মি., XY = 4 সে.মি., YZ = 6 সে.মি., ZW = 5 সে.মি., ∠ w = 45°এ চতুর্ভুজটি কি অনন্য? (গ) KLMN ও WXYZ চতুর্ভুজের অনুরূপ বাহুগুলোর অনুপাত সমান কি? (ঘ) KLMN ও WXYZ চতুর্ভুজের অনুরূপ কোণগুলো পরিমাপ কর। সেগুলো কি পরস্পর সমান? (ঘ) KLMN ও WXYZ সদৃশ কি? |
লক্ষণীয় যে, দুটি সদৃশ চতুর্ভুজের
(ক) অনুরূপ কোণগুলো সমান এবং
(খ) অনুরূপ বাহুগুলো সমানুপাতিক।
দুটি চতুর্ভুজের অনুরূপ বাহুগুলো সমানুপাতিক হলে চতুর্ভুজ দুটি সদৃশ।
কাজ ১। নিচের চিত্রগুলোর সদৃশ জোড় চিহ্নিত কর। তোমার উত্তরের পক্ষে যুক্তি দাও।  |
উদাহরণ ১। ABC সমবাহু ত্রিভুজের AD, BE ও CF তিনটি মধ্যমা।
(ক) একটি সমকোণী সমদ্বিবাহু ত্রিভুজ অঙ্কন কর।
(খ) দেখাও যে, ∠A = ∠B = ∠C
(গ) প্রমাণ কর যে, AD = BE = CF
(ক)

ABC সমকোণী সমদ্বিবাহু ত্রিভুজের AB = BC
(খ)
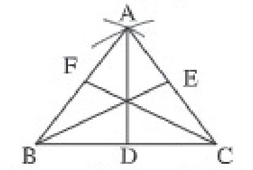
দেওয়া আছে, ABC সমবাহু ত্রিভুজের AB = AC = BC
প্রমাণ করতে হবে যে, ∠A = ∠B = ∠C
অঙ্কন: AD, BE ও CF তিনটি মধ্যমা অঙ্কন করি।
প্রমাণ: ABD ও ACD এ
AB = AC
BD = CD [∵ AD মধ্যমা]
AD সাধারণ বাহু
∵ ABD = ACD
∠ABD = ∠ACD
অর্থাৎ ∠B = ∠C
অনুরুপে দেখানো যায় যে
∠A = ∠B
∴ ∠A=∠B= ∠C
গ।

বিঃনি: দেওয়া আছে, ABC সমবাহু ত্রিভুজের AD, BE ও CF তিনটি মধ্যমা। প্রমাণ করতে হবে যে, AD=BE=CF
প্রমাণ: AB = AC. ∴ ABC সমবাহু ত্রিভুজ
AB = AC
BF = CE ∵ Fও E যথাক্রমে AB ও AC এর মধ্যবিন্দু।
BEC ও BFC এ
BE = CF
BC = BC সাধারণ বাহু
এবং অন্তর্ভুক্ত ∠BCE = অন্তর্ভুক্ত ∠CBF ∵ ∠B = ∠C
BEC = BFC
. BE = CF
অনুরুপে দেখানো যায় যে, AD=BE
AD = BE = CF
(প্রমাণিত)
১।

চিত্রে ABCD সামান্তরিক। ∠ B = কত?
(ক) ∠ C
(খ) ∠ D
(গ) ∠ A - ∠ D
(ঘ) ∠ C - ∠ D
২। ABC এ ∠ B > ∠ C হলে কোনটি সঠিক?
(ক) BC > AC
(খ) AB > AC
(গ) AC > BC
(ঘ) AC > AB
৩। চতুর্ভুজের চার কোণের সমষ্টি কত?
(ক) ১ সমকোণ
(খ) ২ সমকোণ
(গ) ৩ সমকোণ
(ঘ) ৪ সমকোণ
81 ABC - এ ∠ A = 70° ∠ B = 20°হলে ত্রিভুজটি কী ধরনের?
(ক) সমকোণী
(খ) সমদ্বিবাহু
(গ) সূক্ষ্মকোণী
(ঘ) সমবাহু
৫। নিচের প্রতিটি চিত্রে ত্রিভুজ দুটির সদৃশতার কারণ বর্ণনা কর।

৬। প্রমাণ কর যে, নিচের প্রতিটি চিত্রের ত্রিভুজ দুটি সদৃশ।

৭। দেখাও যে, PTN এবং RWT সদৃশ।

৮। DY রেখাংশ ∠CDW কোণটির দ্বিখণ্ডক। দেখাও যে, CDY ও YDW সদৃশ।

৯। নিচের প্রতিটি সদৃশ ত্রিভুজ জোড়া থেকে y এর মান বের কর।

১০। প্রমাণ কর যে, চিত্রের ত্রিভুজ তিনটি সদৃশ।

১১। চতুর্ভুজ দুটির অনুরূপ কোণ ও অনুরূপ বাহুগুলো চিহ্নিত কর। চতুর্ভুজ দুটি সদৃশ কি-না যাচাই কর।
১২। 1 মিটার দৈর্ঘ্যের একটি লাঠি মাটিতে দণ্ডায়মান অবস্থায় 0.4 মিটার ছায়া ফেলে। একই সময়ে একটি খাড়া গাছের ছায়ার দৈর্ঘ্য 7 মিটার হলে গাছটির উচ্চতা কত?

১৩। ABC সমদ্বিবাহু ত্রিভুজের AB AC এবং D, BC এর মধ্যবিন্দু। DE ও DF যথাক্রমে AC ও AB এর উপর লম্ব।
(ক) তথ্যের আলোকে ABC ত্রিভুজটি অঙ্কন করে D বিন্দুটি চিহ্নিত কর।
(খ) দেখাও যে, AD BC
(গ) প্রমাণ কর যে, DE = DF
১৪। ABC' সমদ্বিবাহু ত্রিভুজের AB=AC, এর অভ্যন্তরে D এমন একটি বিন্দু যেন BDC সমদ্বিবাহু ত্রিভুজ হয়।
(ক) বর্ণনা অনুযায়ী চিত্রটি অঙ্কন কর।
(খ) প্রমাণ কর যে, ∠ZABC = ∠ACB
(গ) দেখাও যে, ∆ABD = ∆ACD
১৫। ∆ABC এ AB = AC এবং BE ও CF যথাক্রমে AC ও AB এর উপর লম্ব।
(ক) বর্ণনা অনুযায়ী চিত্র অঙ্কন কর।
(খ) দেখাও যে, ∠B = ∠C
(গ) প্রমাণ কর যে, BE = CF
common.read_more